Im letzten Schuljahr haben Sie bereits Grundlagen zur Codierungstheorie und in deren informatischer Anwendung, der Datencodierung, kennengelernt. Die wichtigsten Inhalte waren:
- Notwendige Absprachen bei Kommunikationsprotokollen
- Zahlen im Binärsystem und wieso dieses so relevant für Maschinenkommunikation ist
- Die ASCII-Codierung
- Den n-bit-Repetitionscode
- Ein verlustbehaftetes Bildkompressionsverfahren
- Den EAN-8 Code (Barcode)
- Die RGB-Codierung von Farben
Anscheinend gibt es sehr viele verschiedene Codierungen. Es muss also wünschenswerte Eigenschaften geben, die eine „gute“ Codierung möglichst haben sollen. Dies untersuchen wir nun.
- Folgende Aufgaben werden in arbeitsteiliger Partnerarbeit durchgeführt.
Eine Person der Partnergruppe übernimmt die Bearbeitung der Aufgabe zum ASCII-Code und die andere zum Morse-Code. - Anschließend stellen sich die beiden gegenseitig ihre Ergebnisse vor.
- Danach wird die Aufgabe zum 3bit-Gencode zu zweit bearbeitet.
- Füllen Sie zum Abschluss diese Tabelle aus.
Diese Aufgabe ist in Teilen nach einer Idee von Carsten Rohe (Lohne, 2024) erstellt worden
Werden Daten in einem Computersystem gespeichert oder werden diese an einen anderen Rechner übertragen, ist es sinnvoll dies auf eine einheitliche Art und Weise zu tun. Man benötigt hierzu eine Codetabelle, die festgelegt, welcher Code für welches Zeichen stehen soll. Verwenden alle die gleiche Tabelle, so kann man problemlos Daten austauschen.
In den Anfängen des Computerzeitalters erkannte man dies Notwendigkeit schnell und entwickelte dazu den ASCII-Code.
Informieren Sie sich zunächst hier über den ASCII-Code, schauen Sie auch das Video.
- Wofür steht die Abkürzung ASCII und was bedeutet dies auf Deutsch?
- Im Standard-ASCII-Code wird jedes Zeichen durch 7 bit ausgedrückt, d. h. eine Folge von 7 Nullen und Einsen. So steht zum Beispiel die Folge 1100110 für den Buchstaben „f“. Wie viele verschiedene Zeichen kann man theoretisch durch 7 bit darstellen?
- Der erweiterte ASCII-Code hat eine Länge von 8 bit. Warum hat man diese Erweiterung vorgenommen? Zusatz: Eine Weiterentwicklung des ASCII-Codes ist der Unicode. Wie viele Zeichen sind in diesem Code gespeichert? Wie lang ist dann der Code für ein einzelnes Zeichen?
- Übersetzen Sie die ersten beiden Zeilen des folgenden in Dualzahlen dargestellten ASCII-Text. 01001001 01100011 01101000 00100000 01100100 01100101 01101110 01101011 01100101 00101100 00100000 01100001 01101100 01110011 01101111 00100000 01100010 01101001 01101110 00100000 01101001 01100011 01101000 00101110 00100000 01010010 01100101 01101110 01100101 00100000 01000100 01100101 01110011 01100011 01100001 01110010 01110100 01100101 01110011
- Codieren Sie ein selbst überlegtes Wort (maximal 8 Zeichen) mit dem ASCII-Code in Dualzahldarstellung.
- Bei der Übertragung eines ASCII-Textes werden keine Leerzeichen mitgesendet. 010101110110111101000110011001010110010101101110011011000110….. Entscheiden Sie, inwiefern man den Text trotzdem wieder übersetzen/decodieren kann. Kann man von links und/oder von rechts mit einer Übersetzung beginnen?
- Ein Wort im Sinne der Codierung ist hier beim ASCII-Code ein einzeln codiertes Zeichen. Entscheiden Sie, weshalb es von Vorteil ist, dass alle ASCII-Codewörter die gleiche Länge haben.
- Der Sender codiert mit ASCII eine Nachricht: 010101110110111101000110011001010110010101101110011011000110….. Aufgrund von Übertragungsfehlern erhält der Empfänger allerdings: 000101110110111101001110011001010110010101101110011011000110….. Entscheiden Sie, ob und inwieweit der Empfänger einer ASCII-codierten Nachricht Übertragungs-fehler erkennen und/oder korrigieren kann. Hinweis: Auch, wenn die Tabelle unten nicht alle ASCII-Zeichen enthält, muss man davon ausgehen, dass es für jede Variante eines Wortes mit 8 bit und einer führenden Null ein ASCII-Zeichen gibt.
| Zeichen | ASCII-Wert (dezimal) | ASCII-Code (8-Bit) |
|---|
Diese Aufgabe ist in Teilen nach einer Idee von Carsten Rohe (Lohne, 2024) erstellt worden
„Samuel Morse, ein US-amerikanischer Erfinder und Professor für Malerei, Plastik und Zeichenkunst, baute 1833 aus Drahtresten, Blechabfällen und seiner Wanduhr den ersten elektromagnetischen Schreibtelegrafen, später „Morseap-parat“ genannt. Dieser wurde 1837 testweise, mit einem nur die zehn Ziffern umfassenden Code, in Betrieb genommen. Diese Zahlen wurden dann mithilfe einer Tabelle in Buchstaben und Worte übersetzt. Die Erweiterung des Codes um Buchstaben 1838 ist Morses Mitarbeiter Alfred Vail zuzuschreiben, wobei sich der Code nun aus Zeichen von drei Längen und unterschiedlich langen Pausen zusammensetzte. Eine erste Versuchslinie entstand in den USA zwischen Baltimore und Washington im Jahre 1843. Ab 1844 wurde dieser Code auch betrieblich bei US-amerikanischen Eisenbahnen und Telegrafenunternehmen eingesetzt („American Morse Code“). Die erste Überseeleitung zwischen Amerika und Europa wurde 1866 fertiggestellt. Friedrich Clemens Gerke, der Inspektor der Hamburger Telegrafenlinie, schrieb den Morsecode 1848 um, da die verschieden langen Pausen den Code negativ beeinträchtigten. Diese Endfassung des Codes wurde 1865 nach leichter Veränderung in Paris auf dem Internationalen Telegraphenkongressstandardisiert. Genormt wurde der Morsecode von der ITU als „International Morse Code“. Im zweiten Weltkrieg wurde der Morsecode zur Verschlüsselung von Geheimbotschaften von Spionen eingesetzt. Ein amüsantes Beispiel ist die Tarnung von Codes als Stickereien in Modedarstellungen von Damenkleidung. Die Verdrängung des Morsecodes aus den Telegrafennetzen ging einher mit der Einführung von Fernschreibern. Obwohl seine Bedeutung im Funkverkehr noch lange anhielt, wurde er auch dort von anderen Verfahren sukzessive ersetzt.“
Quelle: Text gekürzt von hier.


- Übersetzen Sie den folgenden (International) Morse-Code.
.. -.-. .... -.. . -. -.- . --..-- .- .-.. ... --- -... .. -. .. -.-. .... . .-. . -. . -.. . -.. . ... -.-. .- .-. - . -....- - Codieren Sie Ihren Namen mit dem International Morse-Code.
- Beim „International Morse Code“ gibt es zwei unterschiedliche Signallängen und stets gleich lange Pausen. Beim älteren „American Morse Code“ ist dies teilweise anders. Finden Sie heraus, bei welchen Buchstaben dies der Fall ist. Haben Sie eine Idee, warum der „International Morse Code“ daher besser ist?
- Zwischen den einzelnen Buchstaben müssen beim Morsen kurze Pausen gemacht werden. Warum ist das notwendig?
- Einige Buchstaben besitzen einen kurzen Code, bei einigen ist dieser sehr lang. Begründe, warum dies so festgelegt wurde. Ein Wort im Sinne der Codierung ist hier beim Morse-Code ein einzeln codiertes Zeichen. Geben Sie an, aus wie vielen Zeichen im Mittel jedes Morse-Codewort besteht.
- Der Sender codiert eine Nachricht mit dem Morse-Code:
.. -.-. .... -.. . -. -.- . --..-- .- .-.. ... ---Aufgrund von Übertragungsfehlern erhält der Empfänger allerdings:.- -.-. ..-. -.. . -. -.- . --..-- .- .-.. ... ---Entscheiden Sie, ob und inwieweit der Empfänger einer Morse-codierten Nachricht Übertragungsfehler erkennen und/oder korrigieren kann.
| Zeichen | Morsecode |
|---|---|
| A | .- |
| B | -… |
| C | -.-. |
| D | -.. |
| E | . |
| F | ..-. |
| G | –. |
| H | …. |
| I | .. |
| J | .— |
| K | -.- |
| L | .-.. |
| M | — |
| N | -. |
| O | — |
| P | .–. |
| Q | –.- |
| R | .-. |
| S | … |
| T | – |
| U | ..- |
| V | …- |
| W | .– |
| X | -..- |
| Y | -.– |
| Z | –.. |
| 1 | .—- |
| 2 | ..— |
| 3 | …– |
| 4 | ….- |
| 5 | ….. |
| 6 | -…. |
| 7 | –… |
| 8 | —.. |
| 9 | —-. |
| 0 | —– |
| . | .-.-.- |
| , | –..– |
| ? | ..–.. |
| ‚ | .—-. |
| ! | -.-.– |
| / | -..-. |
| ( | -.–. |
| ) | -.–.- |
| & | .-… |
| : | —… |
| ; | -.-.-. |
| = | -…- |
| + | .-.-. |
| – | -….- |
| _ | ..–.- |
| „ | .-..-. |
| $ | …-..- |
| @ | .–.-. |
Ein Genforscher entwickelte einen Binärcode für Gen-Sequenzen. Die vier Basen der DNA (Adenin, Guanin, Thymin und Cytosin) werden mit den Buchstaben A, G, T und C bezeichnen. Die Basen werden, wie folgt, codiert: A: 00 / G: 01 / T: 10 / C: 11.
- Übersetzen Sie mithilfe dieses Binärcodes die dargestellte Gen-Sequenz. 01 00 10 01 01 10 00 11 01 10 10 00 00 10 00 00 01 10 01 00 01 10 01 01 01 10 11 10 01 10
- Überlegen Sie sich eine eigene kurze Sequenz von maximal 10 Zeichen und codieren Sie diese entsprechend.
- Der Sender codiert die Gen-Sequenz: G G C T A C T G A G T T T G C G T G T C T C T A T C A G Der Empfänger erhält: 01 01 11 10 00 11 11 01 00 01 10 10 10 01 11 01 10 01 10 11 10 11 10 00 10 11 00 01 Übersetzen Sie die erhaltene Sequenz selbst. Entscheiden Sie, ob und inwieweit der Empfänger einer mit dem Gen-Code codierten Nachricht Übertragungsfehler erkennen und/oder korrigieren kann.
- Der Binärcode wird erweitert. Ein zusätzliches Bit, welches die Summe der ersten beiden Bit ist, wird zusätzlich angehängt. (Hinweis: Wenn die beiden Informationsbit gleich sind, ist das zusätzliche bit 0, ansonsten 1.) A: 00 –> 000 / G: 01 –> 011 / T: 10 –> 101 / C: 11 –> 110 Nun erhält der Empfänger in Aufgabenteil c) die Nachricht 011 011 110 101 000 110 111 011 000 011 101 101 101 011 110 011 101 011 101 110 101 110 101 000 101 110 000 011 Übersetzen/Decodieren Sie nun erneut die Nachricht. Entscheiden Sie, ob jeder Fehler erkannt werden kann.
- Als Informationsrate eines Codes bezeichnet man den Anteil der Codezeichen eines Codewortes, welche die eigentlichen Informationen beinhalten. Berechnen Sie die Informationsrate des hier vorgestellten 3-Bit-Codes.
- Recherchieren Sie im Internet, bei welchen Codes „im Alltag“ die Prinzipien der Fehlererkennung und der Fehlerkorrektur verwendet werden.
Grundlage: Das RGB-Farbmodell
Man kann sich diese Farbmischung so vorstellen, als würden je eine Lichtquelle mit rotem, grünem und blauem Licht auf einen Punkt scheinen. Das Licht auf dem Punkt ist dann eine Mischung aus den drei Farben. Die Intensität der jeweiligen Farbe ist umso stärker, je stärker die jeweilige Lichtquelle strahlt.
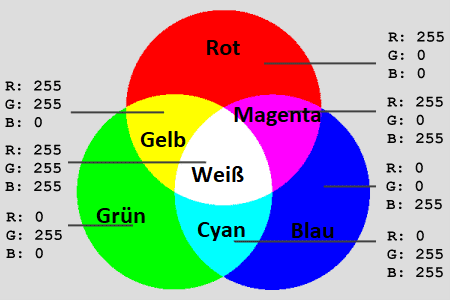
Überschneiden sich zwei Lichtkreise, so entstehen die Sekundärfarben, Gelb, Magenta und Cyan. In der Mitte überschneiden sich alle drei Lichtkreise, wobei die Mischung Weiß erscheint. Die Farbe Schwarz wird durch die Dunkelheit (kein Licht) im umgebenden Raum dargestellt.
Die Farbanteile (r, g, b) werden dabei in Zahlen von 0 bis 255 codiert. So ergeben sich 256⋅256⋅256=28⋅28⋅28=224=16777216 verschiedene Farben.
Für jeden Farbanteil werden aufgrund der 256=28 Möglichkeiten 8 bit, also ein Byte, Speicher benötigt. Da es drei Farbanteile sind, benötigt ein gespeichertes bit eines Bildes somit 3⋅8=24bit, oder 3 Byte.
Beispiele für die binäre Darstellung einiger Farben:
| Farbe | Dezimalwert | Binärwert |
|---|---|---|
| Rot | (255, 0, 0) | (11111111, 00000000, 00000000) |
| Grün | (0, 255, 0) | (00000000, 11111111, 00000000) |
| Blau | (0, 0, 255) | (00000000, 00000000, 11111111) |
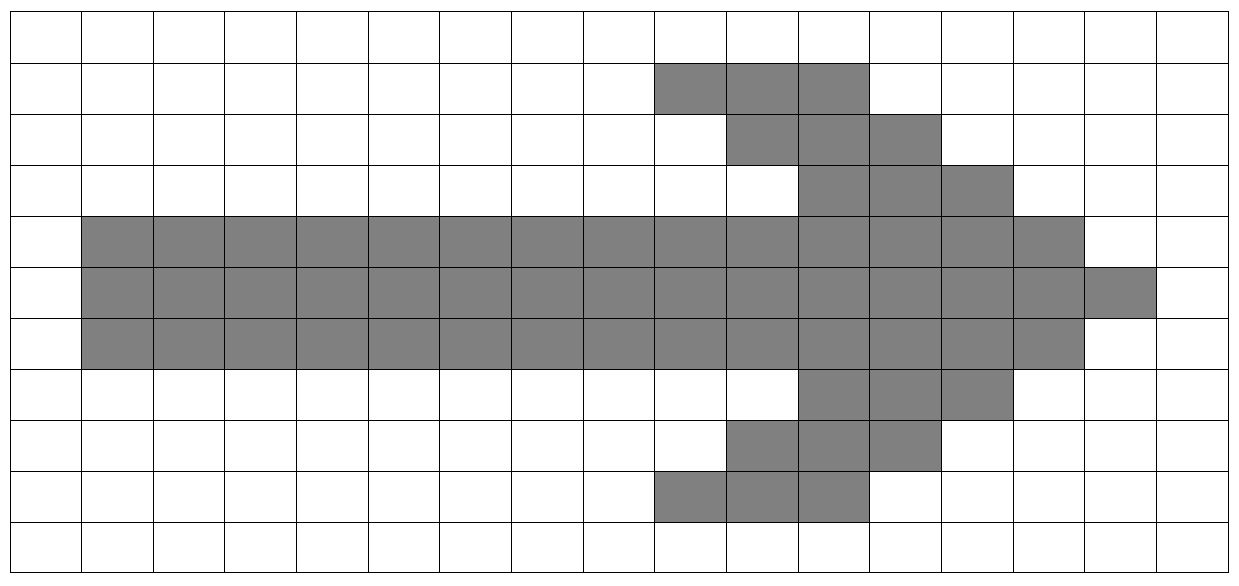
Das Bild „Pfeil“, siehe oben, wird im Bitmap-Format Punkt für Punkt gespeichert. Das bedeutet, je-der Pixel kann mit 0 für weiß und 1 für schwarz einzeln gespeichert werden. Im Bitmap-Format (.bmp) wird jede Farbe mit 8bit gespeichert, durch die Vorabinformation an den Computer, dass 0 weiß und 1 schwarz bedeutet, sparen wir hier bereits Speicherplatz ein. Die zusätzlichen Informationen, z. B. die Maße des Bildes, wer das Bild erstellt hat u. s. w. (die sogenannten Metadaten) werden für unser Verfahren nicht betrachtet. Es werden nur die Einsparmöglichkeiten des Dateikörpers untersucht.
Dateikopf: Zwei Farben, 0 für Weiß, 1 für Schwarz, 17x11 (durch die Information 17x11 weiß der Computer, wann eine Zeile beendet ist.).
Dateikörper:
0000000000000000000000000011100000000000000011100000000000000011100001111111111111100011111111111111100111111111111110000000000000111000000000000011100000000000001110000000000000000000000
Also ist das Bild 11x17 = 187 Bit groß zuzüglich des Speicherplatzes für einen Namen und anderen Zusatzinformationen zur Datei.
Bei einem Schwarz-Weiß-Bild mit der Auflösung 1024 x 768 Pixel ist der Dateikörper bei der Bit-map-Codierung bereits 786432 Bit groß. Ist es möglich, die Größe des Dateikörpers zu verkleinern, ohne Bildinformationen zu verlieren?
Statt
0000000000000000000000000011100000000000000011100000000000000011100001111111111111100011111111111111100111111111111110000000000000111000000000000011100000000000001110000000000000000000000
kann man auch 26-mal weiß, 3-mal schwarz, 15-mal weiß, 3-mal schwarz, ... schreiben.
- Vervollständigen Sie die so entstehende Reihe (die Abkürzungen mit 26w, 3s,... genügen).
Das erscheint momentan nicht unbedingt kürzer, aber nun wird die folgende Codierung vereinbart: Ein Codewort besteht aus vier Zeichen. Das erste bit legt die Farbe fest (0 für Weiß und 1 für Schwarz). Die folgenden drei bit geben an, wie oft die Farbe wiederholt wird (000 für einmal, 001 für zweimal und so weiter).
Das ergibt die folgende Codetabelle:
| Code (Weiß) | Farbe (Weiß) | Anzahl (Weiß) | Code (Schwarz) | Farbe (Schwarz) | Anzahl (Schwarz) |
|---|---|---|---|---|---|
| 0000 | Weiß | 1 | 1000 | Schwarz | 1 |
| 0001 | Weiß | 2 | 1001 | Schwarz | 2 |
| 0010 | Weiß | 3 | 1010 | Schwarz | 3 |
| 0011 | Weiß | 4 | 1011 | Schwarz | 4 |
| 0100 | Weiß | 5 | 1100 | Schwarz | 5 |
| 0101 | Weiß | 6 | 1101 | Schwarz | 6 |
| 0110 | Weiß | 7 | 1110 | Schwarz | 7 |
| 0111 | Weiß | 8 | 1111 | Schwarz | 8 |
- Codieren Sie das Bild "Pfeil" der vorherigen Seite mit dieser Tabelle.
- Dekodieren Sie die folgenden Daten für ein Bild mit 8 Pixel Breite und 11 Pixel Höhe. 0111-0111-0001-1011-0110-1000-0110-1000-0101-1001-0100-1000-0101-1000-0110-1011-0111-0111-0001
- Die bisher verwendete Form der Lauflängencodierung bestand aus Codeblöcken von je vier bit. Entwickeln Sie eine Codetabelle für eine Gesamtblocklänge von drei bit.
- Vergleichen Sie den 4-bit-Code mit dem 3-bit-Code. Untersuchen Sie, bei welcher Art von Bild die 4-bit-Codierung von Vorteil ist und bei welcher Art von Bild die 3-bit-Codierung.
Betrachten wir eine Codierung, welche in einem Supermarkt für Artikel genutzt wird. Jeder Artikel erhält eine Ziffernkombination aus acht Ziffern. Die ersten drei Ziffern sind eine Ländernummer, die folgenden vier stehen für die interne Artikelnummer und die letzte Ziffer ist eine sogenannte Prüfziffer. Ein Beispiel: 20954789
| Ländernummer | Artikelnummer | Prüfziffer |
|---|---|---|
| 209 | 5478 | 9 |
Die Prüfziffer berechnet sich folgendermaßen. Zunächst berechnet man eine gewichtete Summe der ersten sieben Ziffern nach der Methode:
| Ziffer | 2 | 0 | 9 | 5 | 4 | 7 | 8 |
| Gewichtung | 3 | 1 | 3 | 1 | 3 | 1 | 3 |
| Ergebnisse | 2*3=6 | 0*1=0 | 9*3=27 | 5*1=5 | 4*3=12 | 7*1=7 | 8*3=24 |
| Summe | 6+0+27+5+12+7+24=81 | ||||||
Die Prüfziffer ist die Ziffer, welche die Summe zum nächsten Vielfachen von 10 ergänzt. Hier: 81+9=90
Aufgabe- Implementieren Sie ein Programm in Scratch, welches aus einer eingegebenen Länder- und Artikelnummer eine entsprechende Prüfziffer erstelle und das gesamte Codewort ausgibt.
- Implementieren Sie ein Programm in Scratch, welches ein eingegebenes Codewort dieser Art auf seine Korrektheit überprüft. Ist die Prüfziffer falsch, soll eine entsprechende Fehlermeldung ausgegeben werden.
- Analysieren Sie, wie viele Fehler diese Codierung sicher erkennen kann.
In einem Bild sind sechs verschiedene Farbtöne enthalten. Die beiden Farben Rot und Schwarz treten sehr häufig auf, Blau und Gelb mit einer mittleren Häufigkeit, grün und violett selten. Um Speicherplatz bei der Codierung zu sparen, sollen Farben, die häufig vorkommen mit einem kurzen Code dargestellt werden, seltene Farben mit einem längeren Code. Hierzu sollen neben einem Standardcode (Code A) zwei weitere Codierungsvarianten (Code B und Code C) betrachtet werden.
| Farbe | Code A | Code B | Code C |
|---|---|---|---|
| Rot | 000 | 00 | 10 |
| Schwarz | 010 | 11 | 11 |
| Blau | 101 | 01 | 00 |
| Gelb | 110 | 0111 | 011 |
| Grün | 100 | 1010 | 0100 |
| Violett | 001 | 11101 | 0101 |
In der folgenden Abbildung ist Code A in einem Codebaum grafisch dargestellt:
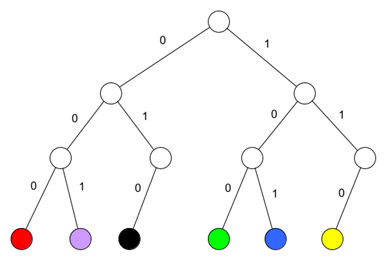
- Erstellen Sie jeweils einen Codebaum für den Code B und den Code C.
- Analysieren Sie, ob sich die Codefolge 110111101000 unter Verwendung der Codes A, B und C jeweils eindeutig decodieren lässt. Warum ist es wichtig, dass das Decodieren eindeutig sein muss?
- Vergleichen Sie die Codebäume der drei Codes A, B und C miteinander: Lässt sich an der Struktur des Baums eine grundsätzliche Problematik für das Decodieren erkennen? Was bedeutet dies für die Notwendigkeit, Trennzeichen (Pausen) zwischen den Codes der einzelnen Farbwerte verwenden zu müssen?
Möchte man nun ein Bild auf einem Computer speichern, so wird für jedes einzelne Pixel „notiert“ welche Farbe dieses besitzt. Das geschieht in der Regel durch eine Binärcodierung, also durch eine eindeutige Folge von Nullen und Einsen. Für das nebenstehende Bild wurde die folgende Codefolge festgelegt:
00 00 00 00 00 00 01 01 01 00 00 01 10 01
00 00 01 01 01 00 00 00 00 00 00
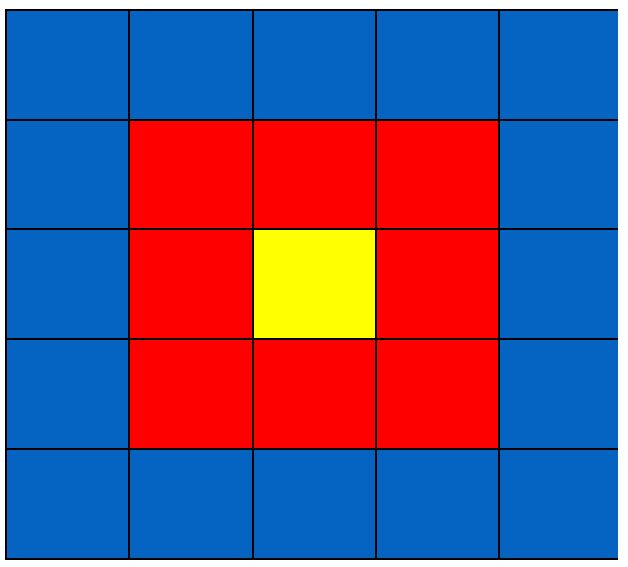
Wenn in einem Bild eine Farbe häufig direkt nacheinander vorkommt, kann man viel Speicher spa-ren: Man gibt einfach an, wie oft eine bestimmte Farbe hintereinander vorkommt. Diese Anzahl nennt man Lauflänge. Dann muss man nicht für jedes Pixel einzeln die Farbe notieren. Hierzu be-nötigt man neben der Codetabelle für die Farben noch eine Codetabelle für die Anzahl.
| Farbe | Code |
|---|---|
| Blau | 00 |
| Rot | 01 |
| Gelb | 10 |
| Lauflänge | Code |
|---|---|
| 1 | 00 |
| 2 | 01 |
| 3 | 10 |
| 5 | 11 |
Notiert man nun zuerst die Anzahl und dann den zugehörigen Farbwert, ergibt sich in Zeichen-schreibweise zunächst die Codefolge 5b6r3g6r5b. Da die Lauflänge 6 nicht in der Tabelle ent-halten ist, muss man diese zusammensetzen. Eine Möglichkeit ist die folgende Codefolge: 5b3r3r3g3r3r5b.Ersetzt man die Zeichen dann noch durch die zugehörigen Binärcodes, erhält man die finale Codefolge: 1100100110011010100110011100.
Hinweis: In der Codetabelle für die Lauflängen kann man beliebige Werte verwenden. Wichtig ist nur, dass man alle möglichen Lauflängen codieren kann. Im vorliegenden Beispiel kann man z. B. die Lauflänge 6 durch 3+3 oder auch durch 5+1 (oder etwas ungeschickt durch 1+1+2+2 oder …) zusammensetzen.
- Zeichnen Sie zwei 5x5-Bilder mit vier Farben (rot, grün, blau, orange). In einem Bild soll es viele Farbwech-sel geben, beim anderen sollen die Farben jeweils häufig aufeinander folgen.
- Geben Sie eine passende Codetabelle für die Farben an und notiere eine Standardcodierung für die beiden Bilder.
- Geben Sie eine Lauflängencodierung für die beiden Bilder an. Erstelle hierzu zunächst eine passende Tabelle für die Lauflängen.
- Bestimmen Sie für die Bilder jeweils die Codelänge bei der Standardcodierung und bei der Lauflängencodierung. Berechne, um viel Prozent der Code kürzer (oder sogar länger) geworden ist.
- (Zusatz) Bei der Datenübertragung eines binären Lauflängencodes wird ein einzelnes Bit falsch übertragen. Untersuche, welche Auswirkungen dies auf die Darstellung des Bildes hat. Welche Auswirkungen hat ein solcher Fehler bei einer Standardcodierung?
Bei der Lauflängencodierung wird ein Bildcode bei geschickter Codierung kürzer. Da man keine Informationen über das Bild verliert, spricht man hier von einer verlustfreien Kompression. Bei „richtigen“ Fotos auf dem Handy (jpg-Dateien) werden noch weitere Kompressionsverfahren verwendet, die zwar viel Speicher sparen, aber auch zu Informationsverlust führen. Solche Verfahren nennt man verlustbehaftet.
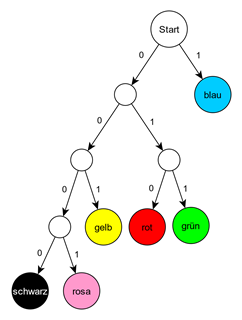
Betrachtet man die Tabelle für den Morsecode, sieht man, dass Buchstaben wie E und N sehr kurze Codes besitzen und das Q hingegen einen langen Code. Da bestimmte Buchstaben in unserer Sprache häufiger vorkommen als andere, kann man so beim Codieren viel Speicher (und Zeit) sparen. Eine solche Art der Codierung nennt man Entropiecodierung. Das gleiche Prinzip kann man auch bei anderen Anwendungen benutzen, z. B. beim Codieren von Bildern. Man zählt, wie häufig einzelne Farbwerte vorkommen und weist ihnen dann einen passenden Code zu.
| Farbe | Anzahl | Code |
|---|---|---|
| Blau | 18 | 1 |
| Grün | 8 | 011 |
| Rot | 7 | 010 |
| Gelb | 4 | 001 |
| Rosa | 3 | 0001 |
| Schwarz | 2 | 0000 |
Beim Morsen muss man zwischen den einzelnen Buchstaben eine Pause machen, da man die Buchstaben sonst nicht unterscheiden kann. Ohne Pausen könnte die Codefolge ∙ ∙ - ∙ ein F sein oder auch EAE bedeuten.
Stellt man eine Codetabelle „geschickt“ auf, dann kann man auf diese Pausen verzichten. In der obenstehenden Codetabelle findest du einen Code, bei dem keine Pause bzw. kein Leerzeichen ge-macht werden muss, da keine Verwechslungsgefahr besteht. Einen solchen Code nennt man präfixfrei. Neben der Tabelle ist der zugehörige Codebaum angegeben. Alle Codes stehen am Ende ei-nes Pfades. Wenn das der Fall ist, dann ist der Code auf jeden Fall präfixfrei.
- Zeichnen Sie ein Bild der Größe 10 x 10 Pixel mit neun verschiedenen Farben.
- Erstellen Sie eine Codetabelle, bei der jeder Farbcode die gleiche Länge besitzt. Geben Sie dann an, wie viele Bits für das gesamte Bild benötigt werden.
- Erstellen Sie eine Codetabelle, bei der die Farben, die häufig vorkommen, einen kurzen Code bekommen. Farben, die selten vorkommen, erhalten dann einen längeren Code. Achten Sie darauf, dass ihr Code präfixfrei ist. Zeichnen Sie zur Überprüfung auch den zugehörigen Codebaum.
- Berechnen Sie mit ihrer Codetabelle zu c) wie viele Bits für das Codieren des gesamten Bildes notwendig sind. Vergleichen Sie mit ihrem Ergebnis aus b).
- (Zusatz) Eine optimale Codierung bzgl. der Häufigkeiten der einzelnen Farben lässt sich systematisch durch das Erstellen eines Huffman-Baums erstellen.
Betrachten Sie für eine Beschreibung des Verfahrens die beiden Videos:
Erstellen Sie dann systematisch eine Codierung für die Farbwerte in der obigen Tabelle mithilfe eines Huffman-Baums. Vergleichen Sie mit ihrer Lösung zu c).
Farben werden technisch häufig durch zwei unterschiedliche Farbcodierungen beschrieben:
Subtraktive Farbmischung: Im Bereich der Drucktechnik benutzt man das Prinzip der subtraktiven Farbmischung. (Weißes Papier → Durch das Mehrfache Auftragen von Farben wird es immer dunkler → Das entspricht einer Subtraktion von Licht). Grundfarben sind hier Cyan (C), Magenta (M) und Gelb (Y). Häufig nimmt man reines Schwarz (K) mit hinzu. Dann spricht man von CMYK. Die Farben sind z. B. von Druckerpatronen oder Tonerkartuschen bekannt.
Additive Farbmischung: Bei selbst leuchtenden Medien, wie z. B. Monitoren, Fernsehern oder Displays verwendet man das Prinzip der additiven Farbmischung. (Dunkler Bildschirm → Durch das Mischen von Lichtpunkten (Pixeln), die sich optisch überlagern, wir das Bild immer heller → Das entspricht einer Addition von Licht.) Als Grundfarben verwendet man hier Rot (R), Grün (G) und Blau (B). Man spricht daher auch von einer RGB-Farbdarstellung.
Stellt man die additive (links!) und die subtraktive (rechts!) Farbmischung in einem Farbkreis dar, so muss man beachten, dass sich die Farben völlig unterschiedlich „mischen“. Es wird durch das Mischen die Helligkeit erhöht oder es reduziert sich die Helligkeit:
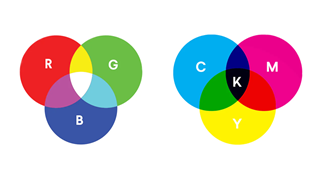
Das Farbschema RGB entspricht unserem natürlichen Sehen. Das menschliche Auge besitzt für das Farbsehen drei verschiedene Zapfensorten, die auf unterschiedliche Farbbereiche reagieren und zusammen einen Farbeindruck erzeugen. Da diese Werte erst noch durch das Gehirn interpretiert werden, ist das Farbensehen sehr subjektiv.
- Informieren Sie sich hierzu im folgenden Video, gucken Sie dieses bis zum Ende:
In der Computertechnik werden Farbwerte der Grundfarben (RGB) häufig in einer 8-Bit-Codierung gespeichert. Das heißt, dass die einzelnen Grundfarben 28=256 mögliche Werte besitzen, von 0 bis 255. Bei 0 ist die Grundfarbe nicht vertreten. Bei 255 ist die Grundfarbe maximal hinzugefügt.
Das kann man beispielhaft wie folgt interpretieren:
Die Farbe in der Tabelle wird als 100001011 00001011 11111010 im Computer gespeichert. Als Dezimalfarbwerte erhält man Rot: 139, Grün: 11; Blau: 250. Das ist etwas Rot, nahezu kein Grün, viel Blau. Mischt man die Farben, ergibt sich Violett ( ).Grundfarbe Rot Grün Blau Sättigung Prozent 54,5 4,3 98,0 Binär 10001011 00001011 11111010 Dezimal 139 11 250 - Vervollständigen Sie die folgende Tabelle mithilfe des RGB-Farbmischers:
Rot: 128Grün: 128Blau: 128
Rot Grün Blau Farbton
Wir wollen nun versuchen, das Codieren eines Farbbildes mit Scratch zu programmieren. Lade Sie diese Datei herunter und starten Sie diese in Scratch. Dort gibt es bereits ein zu codierendes Bild auf der Bühne vorgegeben, sowie das Grundgerüst des Codierungsprogramms.
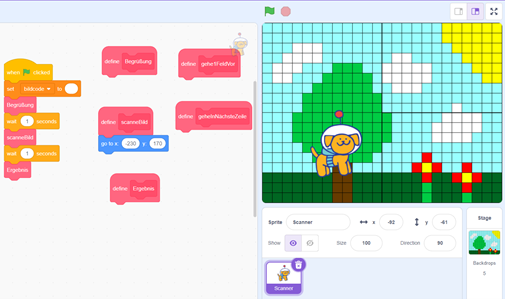
- Mit dem Block "Begrüßung" soll der Scanner eine Begrüßung nach dem Programmstart sagen.
Der Block "Ergebnis" soll am Schluss Informationen über die Maße des Bildes, die Anzahl der Pixel und auch das codierte Bild sagen.
Implementieren Sie diese Funktionalität in den Blöcken "Begrüßung" und "Ergebnis". - Mit dem Block "gehe1FeldVor" soll der Scanner genau ein Pixel weitergehen. Die Pixel sind im¬mer 20 Schritte auseinander.
Mit dem Block "geheInNächsteZeile" soll der Scanner eine Zeile weiter nach unten und zum ganz linken Pixel gehen. Hinweis: Der Scanner startet im Pixel oben links, bei x=-230 und y=170.
Implementieren Sie diese Funktionalität in den Blöcken "gehe1FeldVor" und "geheInNächsteZeile". - Der Block "scanneBild" soll nun das Einlesen der Pixel und den Aufbau des Codes unter der Variablen bildcode übernehmen.
Standardvariante Schwierigere Variante Ziel ist es, für jede Farbe einen entsprechenden Buchstaben als Code zu nutzen und damit den Code bildcode aufbauen. Für die Farbe Rot kann man z. B. den Code "r" nehmen. Der Scanner soll zeilenweise arbeiten und während des Scannens ein anderes Kostüm anziehen. Implementieren Sie diese Anforderungen. Ziel ist es, für jede Farbe einen entsprechenden Buchstaben als Code zu nutzen und damit den Code bildcode aufbauen. Für die Farbe Rot kann man z. B. den Code "r" nehmen. Lauflängen sollen ebenfalls berücksichtigt werden. Also wird für z. B. 10 aufeinanderfolgende rote Pixel das Codewort 10r gespeichert. Der Scanner soll zeilenweise arbeiten und während des Scannens ein anderes Kostüm anziehen. Implementieren Sie diese Anforderungen.

